Train a PINN (Physics Informed Neural Network) with a custom PDE

import torch
import scipy
import numpy as np
import matplotlib.pyplot as plt

from cetaceo.models import MLP
from cetaceo.models.pinn import BoundaryCondition
from cetaceo.models.pinn import PINN
from cetaceo.pipeline import Pipeline
from cetaceo.evaluators import RegressionEvaluatorPlotter
from cetaceo.plotting import TrueVsPredPlotter
from cetaceo.data import TorchDataset

from pathlib import Path

data_dir = Path.cwd().parent / 'sample_data'

We will solve a Burgers equation:

\[\frac{\partial u}{\partial t} + u\frac{\partial u}{\partial x} = \nu\frac{\partial^2u}{\partial x^2}, \qquad x \in [-1, 1], \quad t \in [0, 1]\]

with the Dirichlet boundary conditions and initial conditions

\[u(-1,t)=u(1,t)=0, \quad u(x,0) = - \sin(\pi x)\]

The reference solution is here: https://github.com/lululxvi/deepxde/blob/master/examples/dataset/Burgers.npz

Define the collocation points

We define 256 points on x and 100 points on t. Then, 5000 points are chosen to train the PINN.

POINTS_ON_X = 256
POINTS_ON_T = 100
num_train_simulations = 5000
t = np.linspace(0, 1, POINTS_ON_T)
x = np.linspace(-1, 1, POINTS_ON_X)
T, X = np.meshgrid(t, x)

idx = np.random.choice(X.flatten().shape[0], num_train_simulations, replace=False)
TX = np.concatenate([T.reshape(-1, 1), X.reshape(-1, 1)], axis=1)
train_TX = TX[idx]

device = 'cuda' if torch.cuda.is_available() else 'cpu'

Define the PDE

class BurgersPINN(PINN):
    def __init__(self, viscosity=0.01, *args, **kwargs):
        super().__init__(*args, **kwargs)
        self.viscosity = viscosity

    def pde_loss(self, pred, *input_variables):
        t, x = input_variables
        u = pred
        u_t = torch.autograd.grad(u, t, grad_outputs=torch.ones_like(u), create_graph=True)[0]
        u_x = torch.autograd.grad(u, x, grad_outputs=torch.ones_like(u), create_graph=True)[0]
        u_xx = torch.autograd.grad(u_x, x, grad_outputs=torch.ones_like(u_x), create_graph=True)[0]

        f = u_t + u * u_x - (self.viscosity / torch.pi) * u_xx

        return (f ** 2).mean()

Define the boundary conditions

class InitialCondition(BoundaryCondition):

    def loss(self, pred):
        x = self.points[:, 1].reshape(-1, 1)
        initial_cond_pred = pred
        # the sin is negative because the initial condition is u(0, x) = -sin(pi * x)
        ic_loss = (initial_cond_pred + torch.sin(torch.pi * x).to(device)) ** 2
        return ic_loss.mean()


class XBoudaryCondition(BoundaryCondition):

    def loss(self, pred):
        # as u on the boundary is 0, we can just return the mean of the prediction
        return pred.pow(2).mean()

The points needed on each boundary condition are:

* For the initial condition: The t coordinate must be 0 and the x coordinate should include all of the points on the x domain.

* For the upper and lower boundary conditions: As we have 2 boundaries, there should be 2 tensors, one with x = -1 and t taking all the possible values on its domain and other one with x = 1. Then, both thensors are staked vertically.

initial_points = torch.tensor(x).reshape(-1, 1)
initial_bc = InitialCondition(
    torch.cat([torch.full_like(initial_points, 0), initial_points], dim=-1).float(),
)

boundary_points = torch.tensor(t).reshape(-1, 1)
boundary_bc = XBoudaryCondition(
    torch.cat(
        [torch.cat([boundary_points, torch.full_like(boundary_points, -1)], dim=-1),
        torch.cat([boundary_points, torch.full_like(boundary_points, 1)], dim=-1),]
    ).float()
)

Dataset creation

In this example, a PINN will be trained to learn the PDE just from the equation and some boundary conditions. A way to improve the accuracy of the model, is giving it simulation data on some points. This can be achieved creating datasets that has a value for that data as described on the next cell

Data available at: https://github.com/lululxvi/deepxde/blob/master/examples/dataset/Burgers.npz

data = scipy.io.loadmat(data_dir / 'burgers_shock.mat')

# To train the model with simulation data too, uncomment the following lines
# u_simulation = np.real(data['usol']).flatten().reshape(-1, 1)
# train_dataset = TorchDataset(train_TX, u_simulation[idx])
# test_dataset = TorchDataset(TX, u_simulation)

train_dataset = TorchDataset(train_TX)
test_dataset = TorchDataset(TX)

Train the pinn

input_dim = TX.shape[1]
output_dim = 1 # u(t, x)

net = MLP(
    input_size=input_dim,
    output_size=output_dim,
    hidden_size=40,
    n_layers=4,
    activation=torch.nn.functional.tanh, # With relu the model struggles to converge
)

burgers_pinn = BurgersPINN(
    viscosity=0.01,
    neural_net=net,
    device=device,
)

training_params = {
    'optimizer_class': torch.optim.Adam,
    'optimizer_params': {'lr': 1e-3},
    'epochs': 5000,
    'boundary_conditions': [initial_bc, boundary_bc],
    'print_every': 1000,
}

evaluator = RegressionEvaluatorPlotter(plots_path='.', plotters=[TrueVsPredPlotter()])
pipeline_adam = Pipeline(
    model=burgers_pinn,
    train_dataset=train_dataset,
    test_dataset=test_dataset,
    training_params=training_params
)
model_logs = pipeline_adam.run()
burgers_pinn.plot_training_logs(model_logs)

Epoch 1/5000 Iteration 0. Pde loss: 1.3446e-02, data/bc losses: [5.0211e-01, 1.3750e-02]: 100%|██████████| 1/1 [00:00<00:00,  1.20it/s]
Epoch 1000/5000 Iteration 0. Pde loss: 3.8691e-02, data/bc losses: [5.0880e-02, 5.0844e-04], test loss: 9.2143e-02: 100%|██████████| 1/1 [00:00<00:00, 41.22it/s]
Epoch 2000/5000 Iteration 0. Pde loss: 2.6070e-02, data/bc losses: [3.6652e-02, 2.2149e-04], test loss: 6.6215e-02: 100%|██████████| 1/1 [00:00<00:00, 41.38it/s]
Epoch 3000/5000 Iteration 0. Pde loss: 1.1735e-02, data/bc losses: [1.1807e-02, 1.8047e-04], test loss: 2.8314e-02: 100%|██████████| 1/1 [00:00<00:00, 45.99it/s]
Epoch 4000/5000 Iteration 0. Pde loss: 9.6812e-03, data/bc losses: [6.3920e-03, 7.6869e-05], test loss: 2.0812e-02: 100%|██████████| 1/1 [00:00<00:00, 48.82it/s]
Epoch 5000/5000 Iteration 0. Pde loss: 8.1878e-03, data/bc losses: [4.2261e-03, 1.1524e-04], test loss: 1.6276e-02: 100%|██████████| 1/1 [00:00<00:00, 47.90it/s]

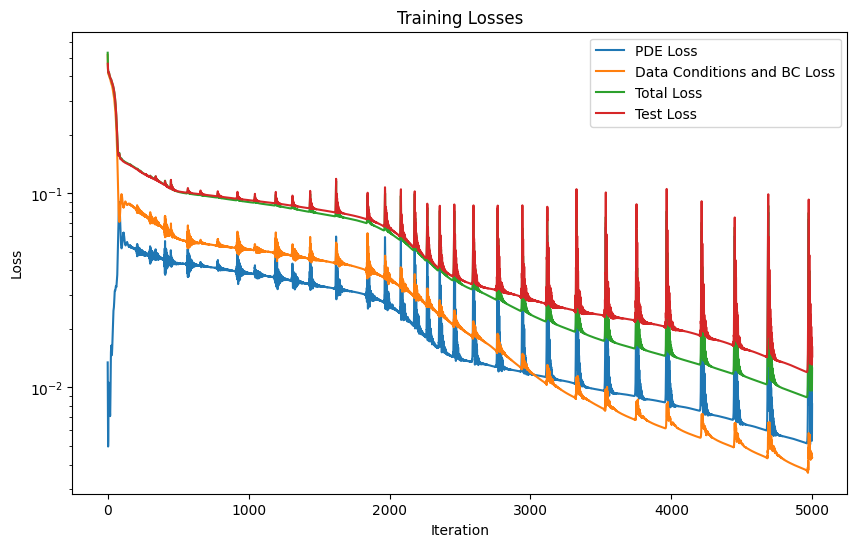
The model is retrained with an LBFGS optimizer to improve its acuraccy

lbfgs_params = {
    'lr': 0.01,
    'max_iter': 12000,
    'max_eval': 10000,
    'history_size': 200,
    'tolerance_grad': 1e-12,
    'tolerance_change': 0.5 * np.finfo(float).eps,
    'line_search_fn': 'strong_wolfe'
}
training_params = {
    'optimizer_class': torch.optim.LBFGS,
    'optimizer_params': lbfgs_params,
    'loaded_logs': model_logs,
    'epochs': 1,
    'boundary_conditions': [initial_bc, boundary_bc],
}

logs = pipeline_lbfgs = Pipeline(
    model=burgers_pinn,
    train_dataset=train_dataset,
    test_dataset=test_dataset,
    training_params=training_params
)
model_logs = pipeline_lbfgs.run()
burgers_pinn.plot_training_logs(model_logs)

Epoch 1/1 Iteration 3100. Pde loss: 1.1975e-04, data/bc losses: [3.1580e-05, 1.7842e-06]: 100%|██████████| 1/1 [01:32<00:00, 92.51s/it]

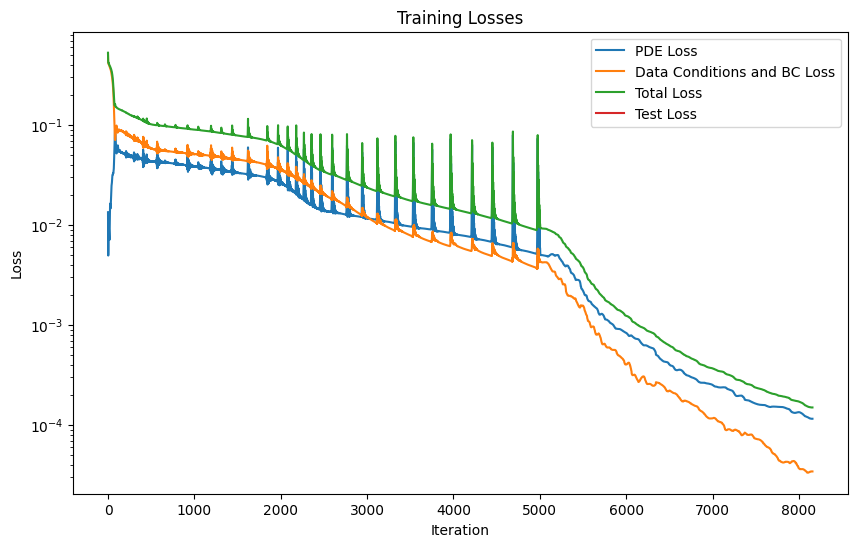
Make the predictions and plot the results

u = burgers_pinn.predict(test_dataset).reshape(POINTS_ON_X, POINTS_ON_T)

u_ref = np.real(data['usol'])

Evaluation using RegressionEvaluator

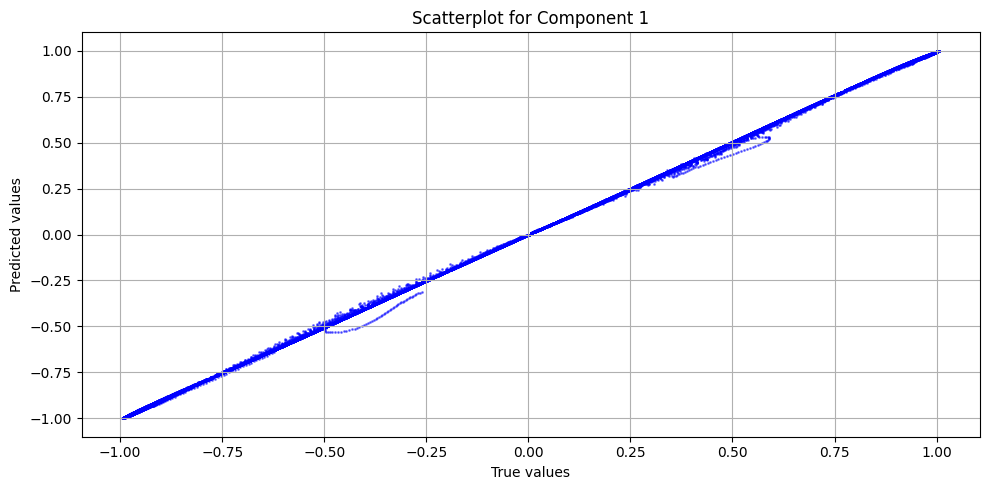
evaluator = RegressionEvaluatorPlotter(plots_path='.', plotters=[TrueVsPredPlotter()])
evaluator(u.reshape(-1, 1), u_ref.reshape(-1, 1))
evaluator.print_metrics()

Regression evaluator metrics:
mse: 4.1491e-05
mae: 0.0039
mre: 1.0112%
ae_95: 0.0086
ae_99: 0.0203
r2: 0.9999
l2_error: 0.0105

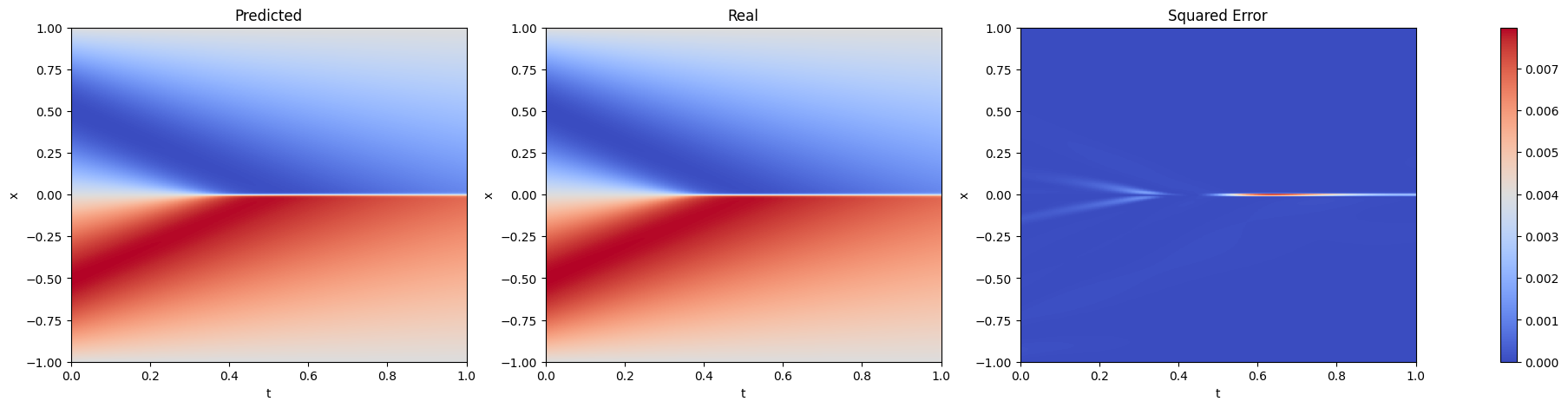
fig, axs = plt.subplots(1, 3, figsize=(25, 5))
for i, (data, title) in enumerate(zip([u, u_ref, (u - u_ref) ** 2], ['Predicted', 'Real', 'Squared Error'])):
    im = axs[i].imshow(data, extent=[0, 1, -1, 1], origin='lower', aspect='0.25', cmap='coolwarm')
    axs[i].set_title(title)
    axs[i].set_xlabel('t')
    axs[i].set_ylabel('x')
    axs[i].set_aspect('auto')
    axs[i].grid(False)

fig.colorbar(im, ax=axs.ravel().tolist())
plt.show()

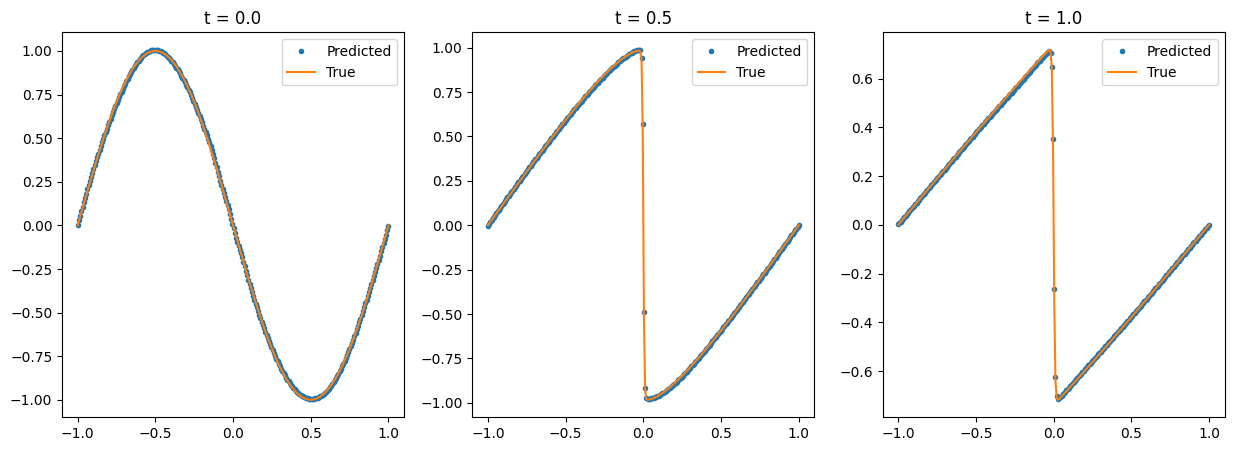
num_time_snapshots = 3
x = torch.linspace(-1, 1, 256).reshape(-1, 1)
fig, axs = plt.subplots(1, num_time_snapshots, figsize=(15, 5))
for i in range(num_time_snapshots):
    instant = i / (num_time_snapshots - 1)
    t = torch.full_like(x, instant)
    u_instant_t = burgers_pinn(torch.cat([t, x], dim=-1).to(device)).detach().cpu().numpy().reshape(-1)
    t_idx = int(np.round((u_ref.shape[1] - 1) * (i / (num_time_snapshots - 1))))

    u_true = u_ref[:, t_idx]
    axs[i].title.set_text(f"t = {instant}")
    axs[i].plot(x, u_instant_t, '.', label='Predicted')
    axs[i].plot(x, u_true, '-', label='True')
    axs[i].legend()

Save and load the model

print("Saving model")
burgers_pinn.save('burgers_pinn.pt')
print("Model saved")
burgers_pinn_loaded = BurgersPINN.load('burgers_pinn.pt', device=device)

print("Model loaded")
predictions = burgers_pinn_loaded.predict(test_dataset)
print(f"Loss: {np.mean((predictions.reshape(-1, 1) - u_ref.reshape(-1, 1)) ** 2)}")

Saving model
Model saved
Model loaded
Loss: 4.1491217538731684e-05